Como calcular matriz inversa + 10 exemplos resolvidos

O que é matriz inversa

A matriz inversa é uma matriz quadrada que multiplicada pela matriz original, é igual a matriz identidade de mesma ordem.

Matematicamente A^-1 x A = I₂ onde:

• A^-1 = matriz inversa de A
• A = matriz A
• I = matriz identidade

Índice da aula:

1. O que é matriz inversa
2. Propriedades
3. Exemplo de matriz inversa 2×2
4. Exemplo de matriz inversa 3×3
5. Exemplo de matriz inversa 4×4
6. Matriz identidade
7. Como calcular matriz inversa
8. Exemplo resolvido 1
9. Exemplo resolvido 2

Para entender essa aula você precisa compreender multiplicação de matrizes.

Propriedades da matriz inversa:

• Se A é a “matriz A” …
• …Então A^-1 é a matriz inversa da “matriz A”
• I₂ é a matriz identidade
• O índice 2 em I₂ significa “matriz de ordem 2“, ou seja, a matriz tem 2 linhas x 2 colunas
• A^-1 x A = I₂ ou seja…
• matriz inversa x matriz = matriz identidade
• Essa lógica de multiplicação acima serve para calcular a matriz inversa
• Existe uma única matriz inversa para cada matriz
• Nem toda matriz possui inversa
• Se o determinante for zero, não há inversa
• A multiplicação de matriz inversa obedece a propriedade comutativa
• Para admitir a inversa, uma matriz tem que ser quadrada

Veja um exemplo de matriz 2×2 com a sua matriz inversa e a sua matriz identidade:

Exemplos de matriz inversa

Exemplo de matriz inversa 2×2:

• Temos uma matriz 2×2
• Temos a matriz inversa, que também é 2×2, obrigatoriamente
• Temos a matriz identidade, que também deve ser 2×2 assim como sua matriz original em questão
• Veja no exemplo que multiplicando a matriz x matriz inversa = matriz identidade

Exemplo de matriz inversa 3×3

• Trata-se de uma matriz de ordem 2
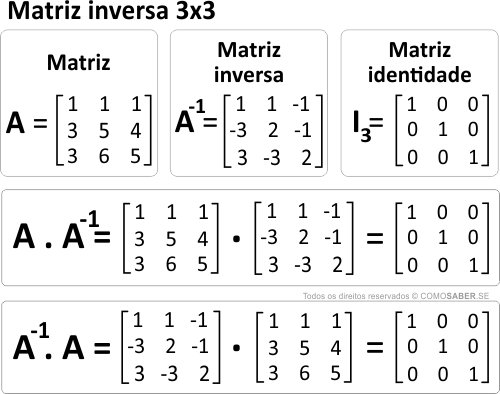
• Veja que a inversa também é 3×3, obrigatoriamente, conforme sua matriz original
• Vemos a matriz identidade, que também deve ser 3×3
• Observamos a propriedade comutativa, onde a matriz x matriz inversa = matriz identidade e vice-versa

Exemplo de matriz inversa 4×4

• Chamamos de matriz de ordem 4
• Se é matriz 4×4 então a matriz inversa também é 4×4
• Da mesma forma a matriz identidade também deve ser 4×4

O que é matriz identidade

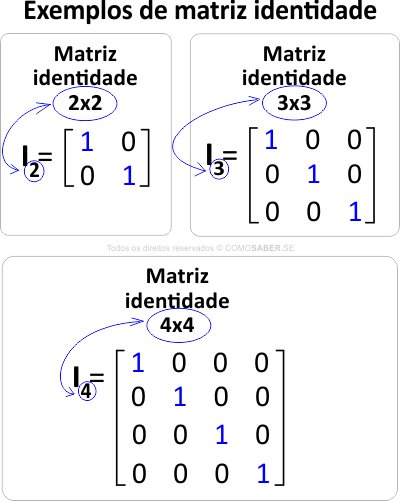
Matriz identidade é a matriz quadrada, de ordem igual a matriz em questão, cujos elementos da diagonal principal tem valor igual a 1 e todos os demais elementos da matriz tem valor igual a zero.

Veja abaixo exemplos de:

• Matriz identidade de ordem 2
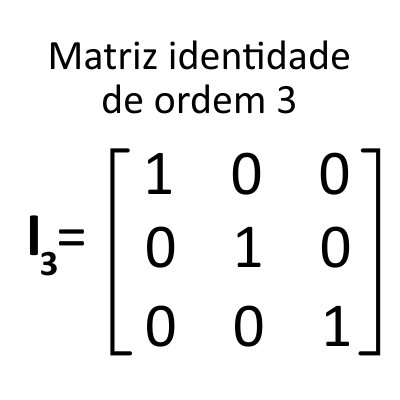
• Matriz identidade de ordem 3
• Matriz identidade de ordem 4

Quer dizer, se ela é identidade, é porque “se identifica com alguma matriz“.

• Se uma matriz for de ordem 2×2, então a sua matriz identidade será também de ordem 2×2
• Se a matriz em questão for de ordem 3×3, então a sua matriz identidade será também de ordem 3×3
• Se a matriz em questão for de ordem 4×4, então a sua matriz identidade será também de ordem 4×4

No exemplo abaixo vemos uma matriz A_2×2 e a sua matriz identidade de ordem 2 correspondente, também 2×2:

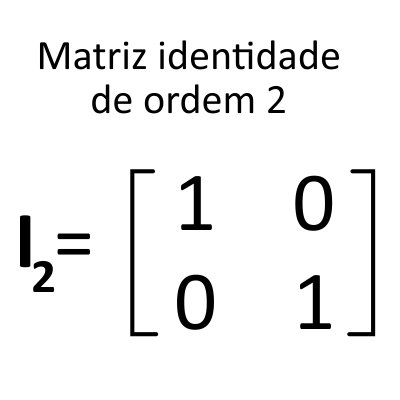
Matriz identidade 2×2:

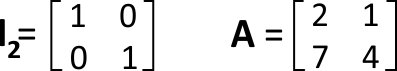
Matriz identidade 3×3:

Informações complementares sobre matriz identidade:

• A matriz identidade sempre é de ordem n ≥ 2, pois não existe matriz de uma só linha e coluna (1×1).

• Todos os elementos da diagonal principal da matriz identidade sempre são iguais a 1

• Todos os demais elementos de uma matriz identidade são iguais a zero

Veja exemplos de matriz identidade 2×2, 3×3 e 4×4:

Propriedade comutativa da multiplicação de matrizes

Na multiplicação de números naturais aprendemos que A x B é a mesma coisa que B x A.

Nas matrizes vale a mesma regra, chamada propriedade comutativa da multiplicação de matrizes:

Portanto, A^-1 x A = A x A^-1

Veja:

Como calcular matriz inversa

Exemplo resolvido 1

Inversão de matrizes pelo método de sistemas lineares

1. Encontrar o determinante, para saber se a matriz possui inversa
2. Multiplicar as matrizes igualando à inversa
3. Resolver as equações lineares

PASSO 1: encontrar o determinante

Encontrar o determinante de uma matriz serve para sabermos se essa matriz tem inversa ou não.

Nem toda matriz admite inversa.

Se o determinante for zero, não tem inversa.

Se o determinante calculado for zero então dizemos que a matriz não é inversível, ou seja, não tem inversa.

Para calcular o determinante de uma matriz 2×2 multiplicamos as diagonais e subtraímos a segunda da primeira, veja:

Veja que o determinante que calculamos é diferente de zero.

Isso quer dizer que podemos calcular a matriz inversa.

PASSO 2: multiplicar e igualar à identidade

Sabendo que A^-1 x A = I₂ vamos montar a conta.

Colocando letras nos lugares dos termos da matriz inversa que vamos calcular.

No nosso exemplo, usamos a, b, c e d. Mas pode ser qualquer letra.

Hora de multiplicar e igualar:

Agora que montamos a conta, vamos multiplicar as linhas x colunas e igualar à identidade.

É uma matriz 2×2 que contém 4 elementos. Então realizaremos 4 cálculos:

1. Começamos multiplicando a linha 1 x coluna 1:

PASSO 3: resolver os sistemas lineares

• Multiplicamos uma das equações
• Cortamos a incógnita de cima com a de baixo
• Isolamos a outra incógnita
• Depois de calcular a e b, substituímos para encontrar c e d

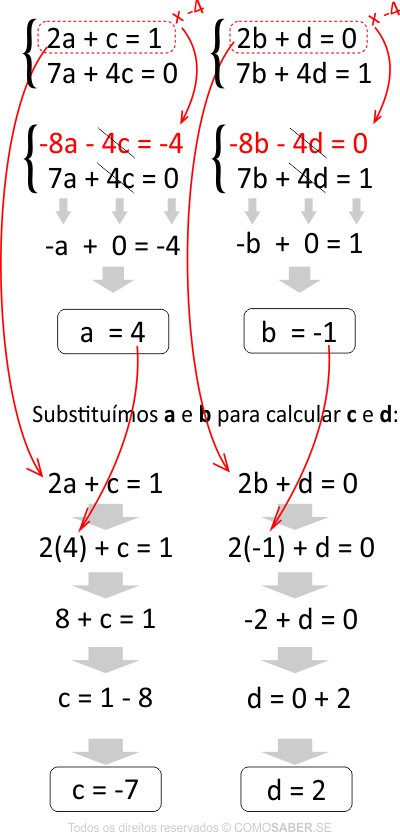
Resultado:

• a = 4
• b = -1
• c = -7
• d = -2

Para finalizar, vamos substituir os valores acima na matriz inversa:

Exemplo resolvido 2:

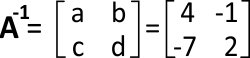
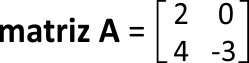
PASSO 1

O determinante é diferente de zero?

Lembre-se: a primeira coisa a fazer é saber se o determinante é diferente de zero, porque se for, não existe inversa e não há o que calcular.

Então vamos calcular o determinante:

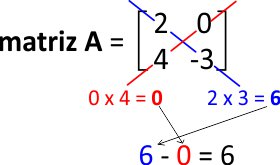
Ou seja, podemos calcular a inversa. Vamos lá.

PASSO 2

Representamos a inversa por A ^-1 e atribuímos algumas letras no lugar dos elementos da matriz.:

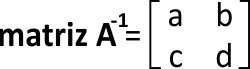
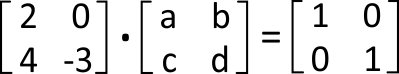
PASSO 3

Vamos multiplicar as matrizes, montando as equações lineares.

• Cortamos os termos multiplicados por zero
• Encontramos a e b

PASSO 4: final

Agora que encontramos a, b, c e d basta colocar os resultados no lugar certo, no lugar as incógnitas da inversa:

Outros métodos para resolução de matriz inversa

Existem outros métodos e teoremas para resolução de matriz inversa.

Umas das formas usuais é pela eliminação de Gauss-Jordan.

O método de eliminação de Gauss-Jordan parte da ideia de se fazer operações entre linhas do sistema.

Essas operações entre linhas são feitas até se chegar em um novo sistema.

Ele transforma o sistema dado em um outro diagonal, isto é, onde todos os elementos fora da diagonal são nulos.

O método de Gauss exigia apenas que se chegasse à forma triangular.

Dando uma olhada breve no método de eliminação de Gauss vemos que não resolvemos um sistema completo da forma 1×1.

O que fazemos é resolver um sistema triangular da forma 1×3.

Na prática, iniciamos com um sistema geral do tipo (2.3) AX = B e finalizamos num sistema do tipo (2.4) A’ X = B’.

Outra forma de resolver é determinando a inversa pela matriz adjunta.

Esse método pode ser interessante se souber os determinantes das sub-matrizes. Mas do contrário não é um método muito prático.