Termos da Multiplicação: 2 Exemplos Resolvidos + aula completa

Conteúdo da matéria:

1. O que é multiplicação
2. Exemplo de Multiplicação
3. Termos da Multiplicação
4. Termos da Multiplicação KIDS
5. Como multiplicar números grandes
6. Exemplos resolvidos de Multiplicação
7. Propriedades da Multiplicação
8. Exercícios resolvidos de multiplicação
9. Macetes com exemplos

O que é Multiplicação

Ao invés de somar 2 + 2 + 2 + 2 + 2 = 10

…você multiplica, assim:

5 x 2 = 10

Ficou mais simples, não é mesmo?

Uma caixa de ovos de 12 ovos. Quantos ovos tem em 4 caixas?

Você pode somar 12 + 12 + 12 + 12 = 48

Ou multiplicar 12 x 4 = 48

• A multiplicação de dois números (exemplo 4 x 12) gera um resultado (nesse caso 48)
• Esse resultado é chamado de produto da multiplicação ou simplesmente produto
• Os dois números que multiplicam são chamados de fatores da multiplicação ou apenas fatores

Exemplo prático de Multiplicação:

Se 1 caixa de ovos tem 12 ovos, quantos ovos tem 4 caixas?

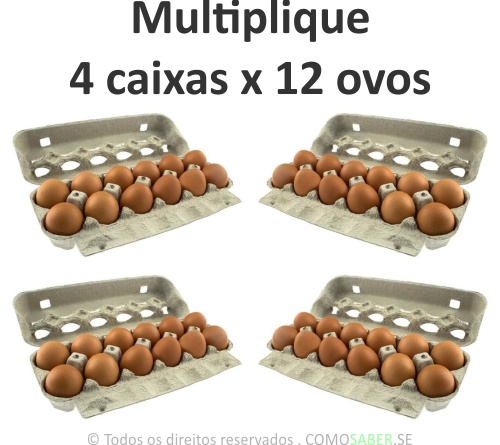
4 x 12 = 48

Explicação:

• Você tem 4 caixas de ovos
• Cada caixa contém 12 ovos
• Quantos ovos você tem no total?
• Veja como resolver:

Ou seja:

4 x 12 = 48

é a mesma coisa que:

12 + 12 + 12 + 12 = 48

Termos da Multiplicação

São 3 os termos da multiplicação:

1. Multiplicador
2. Multiplicando e
3. Produto

Observe e identifique os termos da multiplicação:

• O multiplicador e o multiplicando também são chamados de fatores
• No exemplo acima, o número 4 é o multiplicador
• O número 12 é o multiplicando
• O produto é o resultado da multiplicação
• No exemplo, o produto é 48
• Lembre-se que numerador e denominador são os termos da multiplicação

A multiplicação também pode ser representada dessa maneira:

Termos da Multiplicação

Termos da Multiplicação Kids

Agora de uma forma mais divertida:

Exemplo da Multiplicação Kids

Veja a imagem abaixo.

• São 2 famílias de dinossauros.
• Cada família de 3 dinossauros.

Pergunta: quantos dinossauros tem no total?

Para saber, multiplique 2 x 3 = 6

Observe que 2 x 3 = 6 é a mesma coisa que 3 + 3.

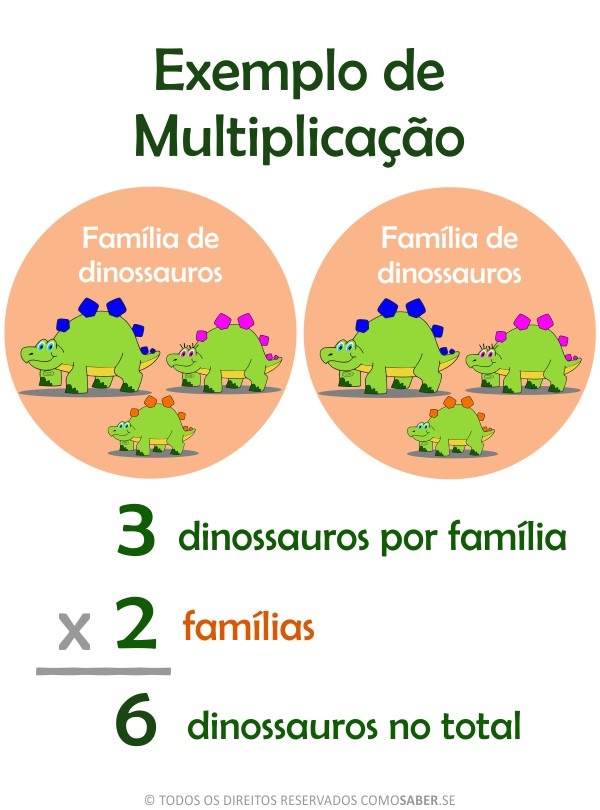
Fatores da Multiplicação Kids

Lembre-se que os dois números que multiplicam também são chamados de fatores ou termos da multiplicação.

Veja na imagem abaixo, de cima para baixo: multiplicando, multiplicador e produto.

Exemplos de Multiplicação

Como resolver

Exemplo 1:

Vamos iniciar com um exemplo simples, 31 x 2

Comece montando a conta, colocando o número maior em cima.

Escreva o resultado abaixo da linha.

Escreva o resultado abaixo da linha.

Propriedades da multiplicação

Quais as 5 Propriedades da Multiplicação?

As 5 propriedades da multiplicação são:

1. Propriedade comutativa
2. Propriedade distributiva
3. Propriedade associativa
4. Elemento neutro
5. Elemento inverso

O que é Propriedade Comutativa da Multiplicação

A propriedade comutativa diz que a ordem dos fatores não altera o produto.

Dados dois números reais a e b, pode-se multiplica-los em qualquer ordem, o resultado será o mesmo.

Ou seja, multiplicar a x b é o mesmo que multiplicar b x a.

Exemplo prático:

3 x 4 = 12
4 x 3 = 12

Dica de estudo: essa propriedade comutativa é válida para número reais e para números complexos. Não se aplica a multiplicação de matrizes.

O que é Propriedade Distributiva da Multiplicação

A propriedade distributiva diz que a soma dos produtos é igual ao produto da soma, de forma que 2 x (3 + 4) = , pode ser resolvido de duas formas: 2 x 7 = 14 ou 6 + 8 = 14.

Veja as duas formas distributivas de resolver:

2 x (3 + 4) = (2 x 3) + (2 x 4) = 6 + 8 = 14
2 x (3 + 4) = 2 x (7) = 2 x 7 = 14

O que é Propriedade Associativa da Multiplicação

A propriedade associativa diz que a ordem que os fatores de uma multiplicação estão associados, não altera o produto. Então 2 x (3 x 4) é igual a 4 x (3 x 2) e igual a3 x (3 x 4).

Veja, a ordem dos fatores não altera o resultado:

• 2 x (3 x 4) = 2 x 12 = 24
• 4 x (3 x 2) = 4 x 6 = 24
• 3 x (4 x 2) = 3 x 8 = 24

Dica de estudo: Você deve sempre resolver o que está dentro dos parênteses primeiro.

O que é elemento neutro da Multiplicação

Elemento neutro da multiplicação é o número 1, pois qualquer número multiplicado por 1 é igual a ele mesmo. Exemplo 8 x 1 = 8.

O que é Elemento Inverso da Multiplicação

Elemento inverso de um número é aquele que multiplicado por este número é igual a 1. Exemplo o inverso de 5 é a fração 1/5, pois multiplicando 5 x 1/5 o resultado é 1.

4. Como multiplicar números grandes

Exemplo resolvido:

Passo 1

Pra começar, coloque os números um em cima do outro. Lembre-se de colocar o número maior em cima, o menor embaixo.

Assim:

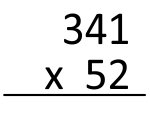
Passo 2

Vamos multiplicar cada algarismo de forma separada.
Começamos a multiplicar os da direita 1 x 2 = 2

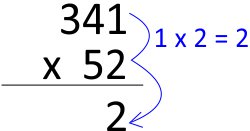
Passo 3

Agora vamos multiplicar 2 x 4 = 8

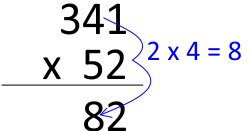
Passo 4

Então devemos multiplicar 2 x 3 = 6

Passo 5

Agora vamos multiplicar o número 5 de baixo por todos os de cima, um de cada vez, começando por 5 x 1 = 5

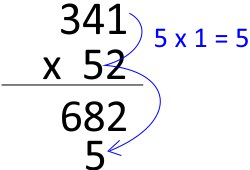
Passo 6

Então multiplicamos o 5 pelo próxio de cima 5 x 4 = 20

Passo 7

Agora vamos multiplicar o último que falta 5 x 3 = 15

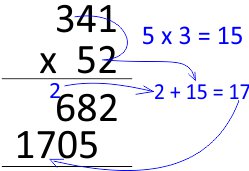
Passo 8

Já multiplicamos todos.

Agora vamos somar 682 de cima com o 1705.

Atenção: não some na calculadora, vai dar errado!

Não se trata de uma soma comum de um + o outro. Veja que nesse caso o número de baixo está deslocado 1 algarismo à direita.

Veja como se deve somar:

• Em azul: 2 + nada = 2
• Em vermelho: 8 + 5 = 13 (vai 1)
• Em preto: 6 + 0 + 1 = 7 (soma também o ‘vai 1’)
• Em roxo: 7 + nada = 7
• Em marrom: 1 + nada = 1
• Resultado final: 17.732

Exercícios de multiplicação com resposta

Lista de exercícios de Multiplicação

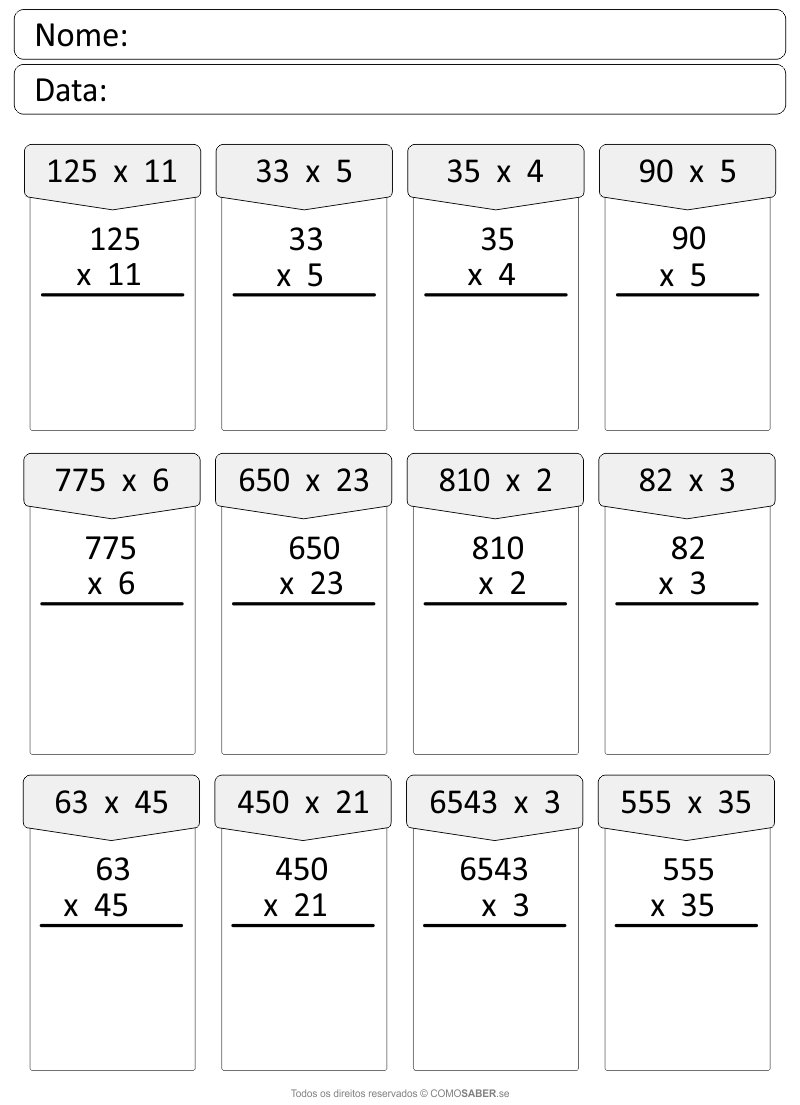
Respostas:

Veja a abaixo a mesma lista, só que agora com respostas / gabarito:

Baixe o PDF da lista de exercícios para imprimir:

Tabuada de multiplicação

A tabuada de multiplicação é o coração de todas as operações de multiplicação.

Antes de aprender multiplicação de fração, você precisa aprender a tabuada de multiplicação.

Isso vale também para multiplicação de matrizes, de potências, de raizes e qualquer outra.

Pra começar os estudos, segue abaixo a tabuada de 1 e a tabuada de 2.

Veja também a tabuada completa aqui, todas as 10 tabuadas.

Tabuada de ‘Vezes’

Macetes de multiplicação

Vamos aprender algumas técnicas.

1. Como multiplicar números maiores x 5

Imagine multiplicar 120 x 5.

Uma forma super prática é “dobrar o 5 pra 10“.

Assim: 120 x 10… ficou fácil agora não? Dá 1.200 porque é só colocar 1 zero no final.

Bem.. mas você dobrou o 5 pra 10…. agora precisa dividir o resultado por 2…. ou seja, 1.200 ÷ 2 = 600

Resultado: 120 x 5 = 600

Veja outros exemplos usando essa técnica:

• 38 x 5 = 38 x 10 = 380 = 380 ÷ 2 = 190
• 22 x 5 = 22 x 10 = 220 = 220 ÷ 2 = 110
• 62 x 5 = 62 x 10 = 620 = 620 ÷ 2 = 310

2. Como multiplicar separando antes

Vamos novamente multiplicar 120 x 5.

Só que agora nós vamos separar unidades, dezenas, centenas, milhares, etc antes.

Assim: 120 é composto por 100 + 20.

Agora podemos multiplicar separado:

• 100 x 5 = 500
• 20 x 5 = 100

Pra finalizar somamos o 500 + 100 = 600

Exemplo 1:

Vamos novamente multiplicar 382 x 5.

Primeiro vamos separar unidades, dezenas, centenas:

382 é composto por 300 + 80 + 2.

Agora podemos multiplicar separado:

• 300 x 5 = 1500
• 80 x 5 = 400
• 2 x 5 = 10

Pra finalizar somamos o 1500 + 400 + 10 = 1.910

Exemplo 2:

Vamos novamente multiplicar 555 x 5.

Primeiro vamos separar unidades, dezenas, centenas:

555 é composto por 500 + 50 + 5.

Agora podemos multiplicar separado:

• 500 x 5 = 2500
• 50 x 5 = 250
• 5 x 5 = 25

Pra finalizar somamos o 2500 + 250 + 25 = 2.775

Exemplo 3:

Vamos novamente multiplicar 218 x 5.

Primeiro vamos separar unidades, dezenas, centenas:

218 é composto por 200 + 10 + 8.

Agora podemos multiplicar separadamente:

• 200 x 5 = 1000
• 10 x 5 = 50
• 8 x 5 = 40

Pra finalizar somamos o 1000 + 50 + 40 = 1.090

Exemplo 4:

Vamos novamente multiplicar 3.351 x 5.

Primeiro vamos separar unidades, dezenas, centenas:

3.351 é composto por 3000 + 300 + 50 + 1.

Agora podemos multiplicar separadamente:

• 3000 x 5 = 15.000
• 300 x 5 = 1500
• 50 x 5 = 250
• 1 x 5 = 5

Pra finalizar somamos o 15.000 + 1500 + 250 + 5 = 16.755

Exemplo 5:

Vamos novamente multiplicar 444 x 5.

Primeiro vamos separar unidades, dezenas, centenas:

444 é composto por 400 + 40 + 4.

Agora podemos multiplicar separadamente:

• 400 x 5 = 2.000
• 40 x 5 = 200
• 4 x 5 = 20

Pra finalizar somamos o 2.000 + 200 + 20 = 2.220

3. Como multiplicar com visão espacial

Imagine empilhar 10 tijolos.

Não dá chamar de parede ainda, mas quase.

Agora imagine fazer uma segunda pilha de tijolos, também com 10 tijolos. Encostamos esses 10 tijolos ao lado dos outros.

Agora, já se parece mais com uma parede.

Vamos colocar mais 3 pilhas iguais. Agora são 5 pilhas de 10 tijolos cada:

Tínhamos 5 pilhas, agora vamos acrescentar mais 20 pilhas, ficamos com 25 pilhas de tijolos.

Quantos tijolos temos agora?

Aí é que entra lógica espacial na hora de multiplicar: 25 x 10

Observe que nessa conta, o número 25 é a quantidade de pilhas de tijolos.

E o número 10 é a quantidade de tijolos em cada pilha.

Multiplicando 25 x 10 saberemos quantos tijolos tem nessa parede. Veja:

25 x 10 = 250 tijolos