Números reais: quais são eles afinal

Índice da aula:

1. O que são números reais
2. Conjunto dos números reais
3. Quais são os números reais
4. Operações com números reais
5. Propriedades dos números reais

O que são números reais

Números reais (R) é o conjunto de números que engloba os números naturais (N), os números inteiros (Z), os números racionais (Q) e os números irracionais (I).

Os Números Reais são representados pela letra R

R = N U Z U Q U I

Na sentença acima, a letra ‘U’ representa união.

Conjunto dos números reais

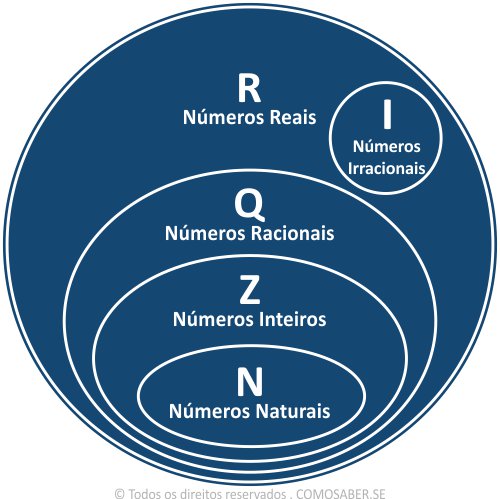
Dentro do conjunto dos números reais estão outros 4 conjuntos:

• Conjunto dos Naturais (N)
• Conjunto dos Inteiros (Z)
• Conjunto dos Racionais (Q)
• Conjunto dos Irracionais (I)

Quais são os números reais

Quais são os números reais então?

Praticamente todos os números são reais.
Os únicos números que não são reais são as raízes de índice par de números negativos como por exemplo

Veja antes quais são os números dos 4 conjuntos, que estão dentro dos números naturais.

Depois é só juntar tudo.

Cada conjunto contém o seguinte:

• Naturais (N): {0, 1, 2, 3, 4, 5, 6…}
• Inteiros (Z): {…, -3, -2, -1, 0, 1, 2, 3,…}
• Racionais (Q): frações e decimais periódicos
• Irracionais (I): decimais não periódicos

Podemos escrever o conjunto de números reais?

Não de uma forma explícita. Veja porque:

• Por um lado, os números naturais e Inteiros são números bem definidos, conforme escrito acima.

• Por outro lado, os números Racionais e Irracionais desdobram-se em frações e decimais infinitos, o que torna impossível escrever os números reais matematicamente em uma sequência, um a um.

Mas afinal qual é o conjunto dos Números Reais?

A resposta é que:

O conjunto dos Números Reais é a junção dos conjuntos de números naturais, números inteiros, números racionais e os números irracionais.

Operações com números reais

As operações com números reais, ou seja, a adição, a subtração, a multiplicação e a divisão, obedecem as seguintes regras:

• A soma de dois números reais é um número real
• A diferença entre dois números reais é um número real
• O produto entre dois números reais é um número real
• O quociente entre dois números reais com divisor diferente de zero é um número real

Propriedades dos números reais

As propriedades dos números reais são idênticas às propriedades estudadas na multiplicação.

São 5 propriedades dos números reais:

1. Propriedade Comutativa
2. Propriedade Associativa
3. Propriedade do Elemento Neutro
4. Propriedade do Elemento Inverso
5. Propriedade Distributiva

1. Propriedade Comutativa

Propriedade Comutativa: A ordem de dois fatores não altera os resultado.

Em uma multiplicação ou soma, a ordem dos números não altera o resultado.

Veja:

3 + 4 = 7
4 + 3 = 7

Importante: a comutatividade não é válida para subtração nem para divisão.

2. Propriedade Associativa

Propriedade Associativa: A ordem de multiplicação ou adição de 3 fatores associados não altera os resultado.

Em uma multiplicação ou soma de 3 fatores associados, a ordem dos números não altera o resultado.

Veja:

(2 + 3) + 4 = 9
(4 + 3) + 2 = 9

Importante: a associatividade não é válida para subtração nem para divisão.

3. Propriedade do Elemento Neutro

Propriedade do Elemento Neutro: Em uma soma o elemento neutro é o zero. Em uma multiplicação o elemento neutro é o 1.

É chamado de elemento neutro porque ele não altera o resultado.

Veja:

3 + 0 = 3
3 x 1 = 3

Importante: o elemento neutro não é válido para divisão de números reais.

4. Propriedade do Elemento Inverso

Propriedade do Elemento Inverso: Em uma soma, o elemento inverso de a é -a. Em uma multiplicação, o elemento inverso de a é 1/a.

Veja:

3 + (-3) = 0
3 x 1/3 = 1

Importante: o elemento inverso não é válido para subtração nem divisão de números reais.

5. Propriedade Distributiva

A propriedade distributiva diz que a soma dos produtos é igual ao produto da soma, de forma que 3 x (2 +5) = , pode ser resolvido de duas formas: 3 x 7 = 21 ou 6 + 15 = 21.

Matematicamente:

a x (b + c) = a x b + a x c