Soma de Frações: Explicação com 4 Exercícios Resolvidos

Aula completa

Conteúdo dessa aula:

1. Como resolver a soma de fração
2. Soma com denominadores iguais
3. Soma com denominadores diferentes
4. Usando MMC
5. Sem usar o MMC
6. Soma de mais de 2 frações

Se precisar, veja antes as noções básicas de fração.

Como resolver a soma de fração

• Soma de frações com denominadores iguais
• Soma de frações com denominadores diferentes

No caso de frações com denominadores iguais, basta somar os numeradores e repetir o denominador. Veja:

Explicamos como calcular esse caso mais abaixo.

Exemplo 1

Soma de frações com denominadores iguais

• Basta repetir o denominador que é o número de baixo
• Então, você deve somar os numeradores, que são os números de cima
• Por fim, simplifique. Veja:

Exemplo 2

Soma de frações com denominadores diferentes

• Método MMC Mínimo Múltiplo Comum
• Método da Multiplicação dos Denominadores

Resolvendo com o método MMC:

Vamos resolver o exemplo 2 usando o Método MMC.

Nesse exemplo, os denominadores são 3 e 5, veja:

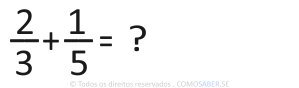
Passo 1:

Calcular o MMC

O primeiro passo é calcular o MMC Mínimo Múltiplo Comum.

Nesse exemplo o MMC é 15. Veja:

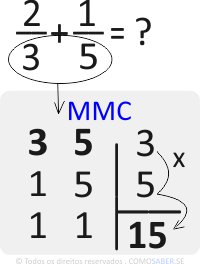
Se não, veja a aula: Como Calcular o MMC Mínimo Múltiplo Comum.

Passo 2:

• Divida o MMC pelo denominador da 1ª fração
• Multiplique o resultado pelo numerador da 2ª fração
• Veja:

Passo 3:

• Divida o MMC pelo denominador da 2ª fração
• Multiplique o resultado pelo numerador da 1ª fração
• Veja:

Passo 4:

Agora é só multiplicar e somar. Confira:

Exemplo 3

Soma com denominadores diferentes

Método sem usar MMC

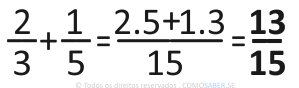
Para que você possa entender mais facilmente, vamos usar exatamente as mesmas frações do exemplo anterior.

Só que agora, com o método da multiplicação:

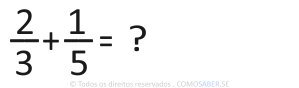
Passo 1:

Multiplique cruzado

• Faça a multiplicação cruzada, como a imagem
• Verdes: multiplique numerador x denominador
• Vermelhos: multiplique numerador x denominador
• Multiplique os denominadores, nesse caso 3 x 5
• Escreva o novo denominador ao lado, o 15

O mesmo para 1 x 3, você deve escrever ao lado.

Fica 2 x 5 + 1 x 3.

Observe também na imagem que está sendo usado um ponto “.” no lugar do vezes “x“.

Tanto o ponto “.” quando o x representam multiplicação.

Passo 2:

Basta somar os numeradores e repetir o denominador:

Resolvido.

Exemplo 4

Soma de 3 frações com denominadores diferentes

Passo 1:

Vamos calcular o MMC

O primeiro passo é calcular o MMC Mínimo Múltiplo Comum.

Nesse exemplo o MMC é 60. Veja:

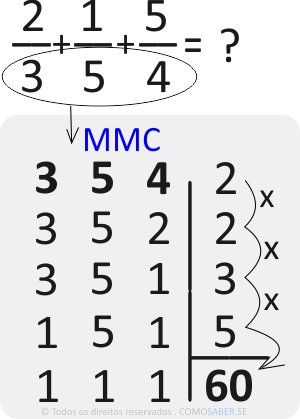
Se não, veja a aula: Como Calcular o MMC Mínimo Múltiplo Comum.

Passo 2:

Divida o MMC pelo denominador da 1ª fração e multiplique pelo numerador da mesma.

Passo 3:

Divida o MMC pelo denominador da 2ª fração e multiplique pelo numerador da mesma.

Passo 4:

Divida o MMC pelo denominador da 3ª fração e multiplique pelo numerador da mesma.

Passo 5:

Basta somar os numeradores e repetir o denominador:

Resolvido.

Subtração de frações

Subtração de frações com denominadores diferentes

Ou seja, temos dois casos na subtração de frações:

• Subtração de frações com denominadores iguais
• Subtração de frações com denominadores diferentes

Para entender melhor veja aula de subtração de frações com exercícios resolvidos.

Veja um exemplo simples de subtração de frações com denominadores iguais:

• Subtração de fração com Método MMC
• Subtração de fração com Método da Multiplicação

Você concluiu a aula de soma de frações.

Veja a aula de subtração de frações com exercícios resolvidos.