Multiplicação de Matrizes: 2 exemplos resolvidos passo a passo

Como fazer a multiplicação de matrizes

Para fazer a multiplicação de matrizes é necessário que o número de colunas de uma matriz A seja igual ao número de linhas da matriz B.

O resultado da multiplicação de uma matriz A por uma matriz B é uma matriz C.

Índice da aula:

1. Como fazer a multiplicação de matrizes
2. Elementos da matriz
3. Linhas e Colunas da Matriz
4. Exemplo 1 resolvido matriz 2 x 2
5. Exemplo 2 resolvido matriz 2 x 3
6. Propriedades da multiplicação de matrizes

Elementos de uma matriz:

Observe a matriz C na imagem abaixo.

Identifique o seguinte:

• A matriz C é do tipo 2 x 2
• Ou seja, tem 2 linhas x 2 colunas
• Toda matriz 2 x 2 tem 4 elementos
• C₁₁ é o 1º elemento da 1ª linha
• C₁₂ é o 2º elemento da 1ª linha
• C₂₁ é o 1º elemento da 2ª linha
• C₂₁ é o 2º elemento da 2ª linha

O 1º algarismo desse 11, no caso o número 1, representa a linha. Já o 2º algarismo representa o número do elemento.

Logo C₁₁ é o 1º elemento da 1ª linha.

Linhas e Colunas da Matriz

Veja como é uma matriz 2 x 2:

Multiplicação de matrizes 2×2

Exemplo 1 resolvido:

Como resolver multiplicação de matrizes 2×2.

Vamos multiplicar uma matriz A (2×2) x matriz B (2×2).

Lembre-se que o resultado será também uma matriz 2×2.

Você vai precisar fazer 4 cálculos:

• Calcular C₁₁
• Calcular C₁₂
• Calcular C₂₁
• Calcular C₂₂

• O número de colunas de uma matriz A é igual ao número de linhas da matriz B?
Resposta: nesse caso sim, são 2 linhas na matriz A e 2 colunas na matriz B. Então podemos resolver!

• Iniciamos multiplicando cada linha da matriz A pelas colunas da matriz B.

Passo 1: multiplicar a linha 1 x coluna 1

Comece multiplicando a linha 1 da matriz A pela coluna 1 da matriz B, conforme a imagem a seguir.

Passo 2:

Agora multiplique a linha 1 da matriz A pela coluna 2 da matriz B:

Passo 3:

Então multiplique a linha 2 da matriz A pela coluna 1 da matriz B:

Passo 4:

Por fim, multiplique a linha 2 da matriz A pela coluna 2 da matriz B:

Pronto! Você já concluiu a multiplicação de matrizes 2×2.

Os valores que calculamos foram:

• C₁₁: 18
• C₁₂: 66
• C₂₁: 13
• C₂₂: 53

Para finalizar, escreva os resultados calculados, de c₁₁, c₁₂, c₂₁ e c₂₂, assim:

Exemplo 2 resolvido:

Multiplicação de matrizes de ordens diferentes

Agora vamos multiplicar uma matriz 2 x 3 X matriz 3 x 2.

Novamente, serão 4 cálculos:

• Calcular C₁₁
• Calcular C₁₂
• Calcular C₂₁
• Calcular C₂₂

• O número de colunas de uma matriz A é igual ao número de linhas da matriz B?
Resposta: nesse caso sim, são 2 linhas na matriz A e 2 colunas na matriz B. Então podemos resolver!

• Iniciamos multiplicando cada linha da matriz A pelas colunas da matriz B.

Passo 1: multiplicar a linha 1 x coluna 1

Comece multiplicando a linha 1 da matriz A pela coluna 1 da matriz B, conforme a imagem a seguir.

Passo 2: multiplicar a linha 1 x coluna 2

Agora multiplique a linha 1 da matriz A pela coluna 2 da matriz B:

Passo 3: multiplicar a linha 2 x coluna 1

Então multiplique a linha 2 da matriz A pela coluna 1 da matriz B:

Passo 4: multiplicar a linha 2 x coluna 2

Por fim, multiplique a linha 2 da matriz A pela coluna 2 da matriz B:

Pronto! Você já calculou os valores.

Os valores que calculamos foram:

• C₁₁: 14
• C₁₂: 27
• C₂₁: 24
• C₂₂: 46

Para finalizar a multiplicação de matrizes, escreva os resultados calculados, de c₁₁, c₁₂, c₂₁ e c₂₂, assim:

Quais as propriedades da multiplicação de matrizes

São 6 as propriedades da multiplicação de matrizes:

1. Propriedade associativa da multiplicação
2. Propriedade distributiva
3. Propriedade do elemento neutro da multiplicação
4. Propriedade do elemento nulo da multiplicação
5. Propriedade das dimensões
6. Matriz inversa

1. Propriedade associativa da multiplicação

A propriedade associativa mostra que a ordem que os fatores estão associados, não altera o resultado.

Assim, as duas multiplicações abaixo geram o mesmo resultado:

(A x B) x C = A x ( B x C).

2. Propriedade distributiva

Na propriedade distributiva a soma dos produtos é igual ao produto da soma, de forma que A x (B + C) = AxB + AxC.

Assim, as duas multiplicações abaixo geram o mesmo resultado:

A x (B + C) = AxB + AxC.

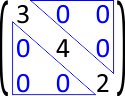
3. Propriedade do Elemento Neutro

O elemento neutro na multiplicação de matrizes é a matriz identidade.

Elemento neutro é aquele que multiplicado por uma matriz quadrada, resulta a própria matriz.

Veja o exemplo:

Matriz identidade de ordem 2:

Matriz identidade de ordem 3:

Exemplo, matriz 2 x 2, matriz 3 x 3, matriz 4 x 4.

Toda matriz A _{n x n} multiplicada pela matriz identidade I _{n x n} será igual a própria matriz A _{n x n}.

A função do elemento neutro na multiplicação de matrizes, tem o mesmo efeito que o elemento neutro número 1 nos números naturais.

Na multiplicação 7 x 1 = 7 o número 1 é um elemento neutro, pois o resultado é igual ao multiplicador 7, nesse caso.

Já na multiplicação de matrizes, como você estudou acima, o elemento neutro é a matriz identidade.

Dúvidas sobre matriz identidade? Estude aqui.

4. Propriedade do Elemento Nulo

Elemento nulo na multiplicação de matrizes é a matriz nula em que todos os elementos são zero “0”.

A matriz nula é representada pela letra O.

A Propriedade do Elemento Nulo diz que qualquer matriz A _{n x n} multiplicada por uma matriz nula O _{n x n} resultada numa matriz nula, onde todos os elementos são zero.

Veja na prática:

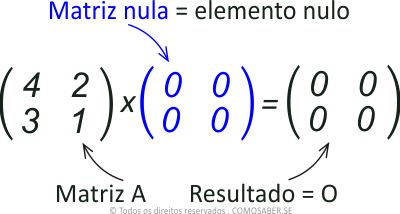
A função de matriz nula é similar a função do número 0 em relação aos números naturais.

Pois veja que qualquer número multiplicado por zero, é igual a zero: 3 x 0 = 0.

Numa multiplicação de matrizes, da mesma forma, a matriz nula também zera o resultado, quando multiplica outra matriz com as mesmas dimensões.

5. Propriedade das Dimensões

Toda matriz A (m x n) multiplicada uma matriz B (n x k) resultará uma matriz C (m x k).

• m = número de linhas da matriz A
• n = número de colunas da matriz A
• n = número de linhas da matriz B
• k = número de colunas da matriz B

Ou seja, a matriz resultante:

• Terá o número de linhas igual ao número de linhas da matriz A
• Terá o número de colunas igual ao número de colunas da matriz B

• 3 linhas… igual a primeira matriz
• 4 colunas… igual a segunda matriz

Na multiplicação de matrizes, onde A é uma matriz 2 x 3 e B é uma matriz 3 x 4, então a matriz resultante será 2 x 4.

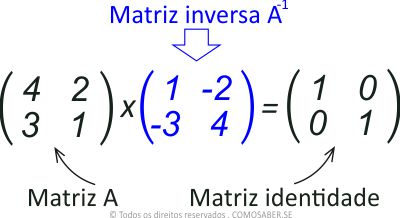
6. Matriz inversa

Uma matriz inversa A é aquela que multiplicada por uma matriz B, resulta uma matriz identidade de mesma ordem.

• matriz A x matriz A^-1 = matriz I_n

Ou seja:

• Multiplicando matriz A X matriz inversa A^-1, o resultado será uma matriz identidade I_n.

Veja o exemplo:

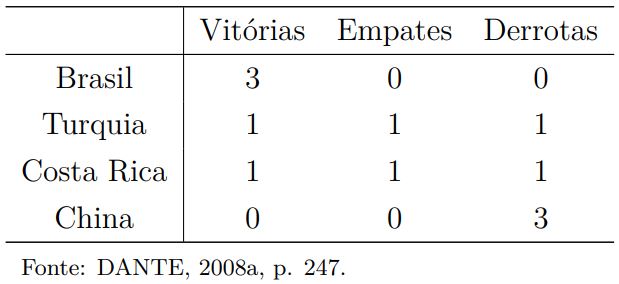
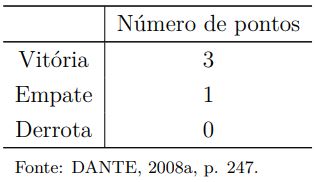
Questão (UEL-PR) – Durante a fase 1 da Copa do Mundo de futebol, fase essa que foi realizada no Japão e na Coréia do Sul no ano de 2002, o grupo C era formado por 4 países. Esses países eram o Brasil, a Turquia, a Costa Rica e a China. Analise os resultados (tanto os números de vitórias, quanto de empates, como de derrotas) de cada país que participou da primeira fase.

Observe que esses resultados constam na tabela e também constam na matriz A4×3 correspondente.

Eis os resultados dos times do grupo C na copa do Mundo de 2002

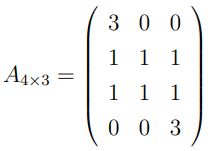
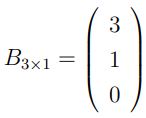
Essa pontuação conquistada pode ser escrita numa tabela matricial, cujos valores são produto da multiplicação de duas matrizes A x B.

A matriz A tem 4 linhas, que representam os 4 países e possui 3 colunas que representam os três tipos de pontuação que cada país teve: 1. vitórias, 2. empates e 3. derrotas.

Já a matriz B representa a pontuação em cada tipo de resultado, sendo 3 pontos para vitória, 1 para empate e 0 para derrota.

Multiplicando as matrizes temos o seguinte:

• Brasil: 3.3 + 0.1 + 0.0 = 9
• Turquia: 1.3 + 1.1 + 1.0 = 4
• Costa Rica: 1.3 + 1.1 + 1.0 = 4
• China: 0.3 + 0.1 + 3.0 = 0

Dessa forma:

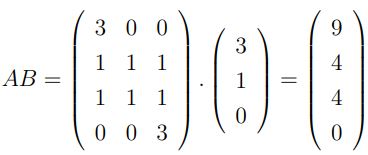
De outra forma, precisamos multiplicar a matriz de resultados individuais pela matriz de pontuação pra cada tipo de resultado.

É importante observar que essa multiplicação de matrizes só é possível porque obedecemos uma regra básica da multiplicação de matrizes: o número de colunas da matriz A_4×3 é igual ao número de linhas da matriz B_3×1.

E como obedecemos a regra, podemos multiplicar, obtendo como resultado uma matriz com o número de linhas igual ao da primeira matriz e o número de colunas igual ao da segunda matriz..

Portanto, a multiplicação das matrizes A e B pode ser representada da seguinte forma:

A_4×3 x A_3×1 = C_4×1

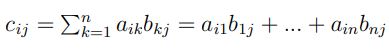
Multiplicação de matrizes por um número real

Para finalizar a aula, vamos ver como resolver a multiplicação de matrizes por um número real.

A multiplicação de uma matriz por um número real é provavelmente a multiplicação mais simples nu mundo das matrizes.

Basta multiplicar o número real R por cada elemento da matriz, não importa quantos elementos a matriz possui.

Matematicamente, multiplicando R x A_2×2, onde R é um número real e A é uma matriz 2×2, basta multiplicarmos o R por cada um dos quatro elementos da matriz A.

Exemplo, veja a matriz:

Finalize praticando os exercícios de multiplicação de matrizes

Isso mesmo, para fixar o conhecimento, finalize praticando os exercícios de multiplicação de matrizes:

• Para fixar o conhecimento, é preciso resolver alguns cálculos por conta própria e conferir o resultado do gabarito.
• Retome a página mais acima e reescreva alguns dos exercícios resolvidos numa folha.
• Faça o passo a passo e procure entender as dimensões das matrizes, a regra de número de colunas da matriz A ser igual ao número de linhas da matriz B.

Um pouco de história sobre matrizes

As matrizes passaram a se chamar matrizes por volta de 1850, denominação definida por Joseph Silvester, um matemático britânico de renome.

O significado essencial de matrizes é o de ser algo onde se cria alguma coisa, uma espécie de fonte geradora ou criadora.

Aplicação da multiplicação de matrizes

Alguns cálculos são mais raramente utilizados. Outros, são de uso mais frequente.

As matrizes certamente são usuais na matemática ou, de forma prática, na engenharia em especial, além de outros campos científicos.

Os cálculos de movimento de corpos rígidos exigem o uso de matrizes para serem calculados.

A probabilidade e estatística, fundamental em aplicações reais todos os dias, dependem em muitos momentos, da presença de matrizes para terem seus cálculos processados.

E vai além: a ótica e o eletromagnetismo, além da eletrodinâmica quântica, também fazem uso.

Quando alguém faz uma pesquisa na internet, os sites que aparecem como resposta da pesquisa, são ordenados utilizando-se, entre outros, de cálculos de matrizes.

Tabela resumo sobre matrizes: