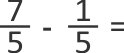Exercícios de Fração: 20 exercícios + gabarito + explicação
Exercício 1)
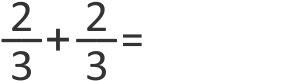
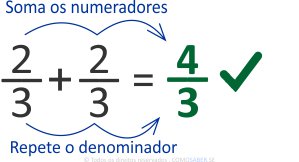
Então, basta somar os números de cima, chamados numeradores 2 + 2 = 4 e repetir o de baixo, chamado denominador: 3.
Exercício 2)


Então, basta somar os números de cima, chamados numeradores 2 + 2 = 4 e repetir o de baixo, chamado denominador: 3.
Por fim, precisamos simplificar a fração.
Veja que ambos são divisíveis por 3, tanto o 12 quanto o 3.
Exercício 3)
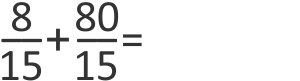

Então, basta somar os números de cima, chamados numeradores: 8 – 80 = 88.
Depois, repetir o de baixo, chamado denominador: 15.
Exercício 4)

Como os denominadores são diferentes, precisamos calcular o MMC pra começar:
Na dúvida, veja a aula de MMC Mínimo Múltiplo Comum.
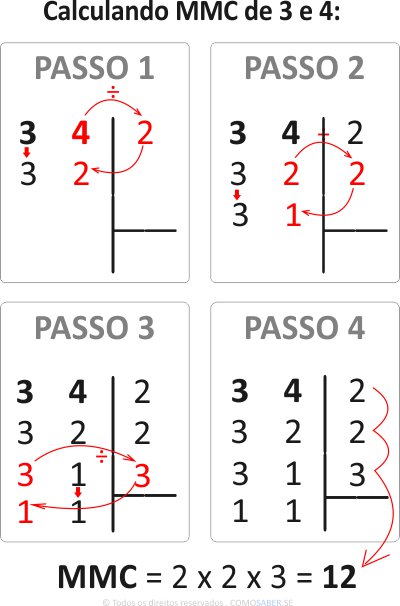
- Divida o MMC 12 pelo denominador 3
- Multiplique pelo numerador 2
- Faça isso com as 2 frações

- 4 x 2 = 8
- 3 x 5 = 15
- 8 + 15 = 23
- Repita o denominador 12, que é o MMC, embaixo:
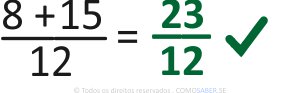
Exercício 5)
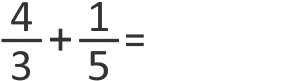
Novamente, os denominadores são diferentes, precisamos calcular o MMC pra começar:
Na dúvida, veja a aula de MMC Mínimo Múltiplo Comum.
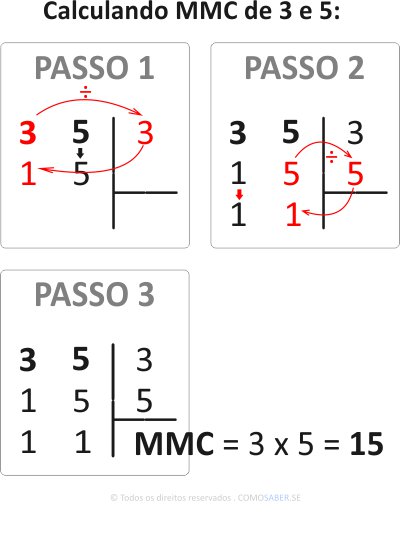
- Divida o MMC 15 pelo denominador 3
- Multiplique pelo numerador 4
- Faça isso com as 2 frações

- 5 x 4 = 20
- 3 x 1 = 3
- 20 + 3 = 23
- Repita o denominador 15, que é o MMC, embaixo:

- Está pronto:

Exercício 1)
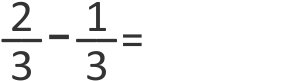

Então, basta subtrair os números de cima, chamados numeradores 2 – 1 = 1 e repetir o de baixo, chamado denominador: 3.
Exercício 2)
Resposta:
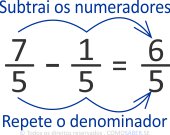
Então, basta subtrair os números de cima, chamados numeradores 7 – 1 = 6 e repetir o de baixo, chamado denominador: 5.
Exercício 3)
Resposta:

E mais uma vez vamos subtrair os números de cima, chamados numeradores: 28 – 27 = 1.
Depois, repetir o de baixo, chamado denominador: 28.
Exercício 4)
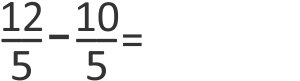
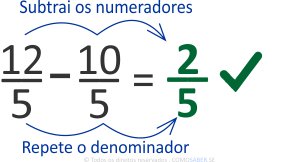
Sendo assim, vamos subtrair os números de cima, chamados numeradores 12 – 10 = 2 e repetir o de baixo, chamado denominador: 5.
Exercício 5)
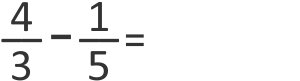
Agora temos uma subtração onde os denominadores são diferentes.
Nesse caso, precisamos calcular antes o Mínimo Múltiplo Comum. Lembra como?
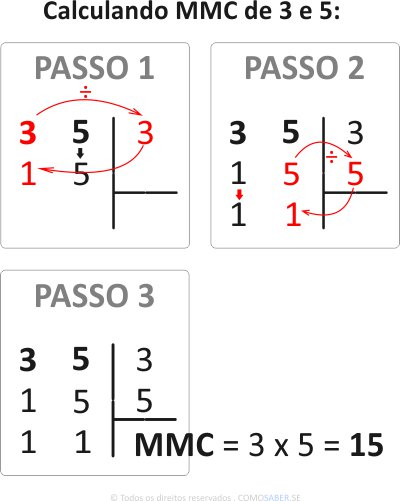
- Depois divida o MMC 15 pelo denominador 3
- Multiplique pelo numerador 4
- Repita o processo com a segunda fração:



Exercício 1)

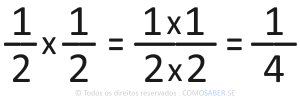
Lembre-se que na multiplicação de frações não importa se os denominadores são iguais ou diferentes.
Em qualquer caso, a multiplicação será direta:
Numerador x numerador
Denominador x denominador
Então, basta multiplicar os números de cima entre eles e depois multiplicar os de baixo entre eles.
Exercício 2)
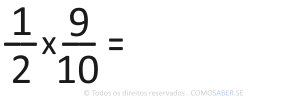

- Multiplicamos 1 x 9 = 9
- Multiplicamos 2 x 10 = 20
Como a fração já está irredutível, não é preciso simplificar.
Está pronto!
Exercício 3)


- Multiplicamos 1 x 2 = 2
- Multiplicamos 3 x 3 = 9
Como a fração já está irredutível, não é preciso simplificar.
Está pronto!
Exercício 4)

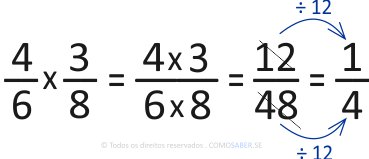
- Multiplicamos 4 x 3 = 12
- Multiplicamos 6 x 8 = 48
Como a fração não está irredutível, é preciso simplificar a fração.
No caso acima, dividimos por 12, tanto o numerador, quanto o denominador.
Exercício 5)

A primeira fração 3 1/5 é uma fração mista.
Antes de multiplicar, precisamos transformar a fração mista em fração imprópria:


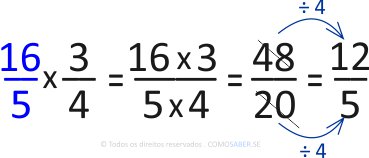
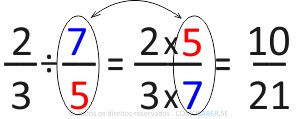
Exercício 1)
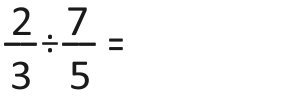
Exercício 2)
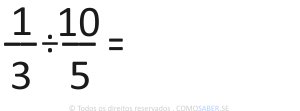

Nesse caso, também simplificamos, pois tanto o 5 quanto 30 são divisíveis por 5.
Exercício 3)


Nesse caso, também simplificamos, pois tanto o 40 quanto 45 são divisíveis por 5.
Exercício 4)

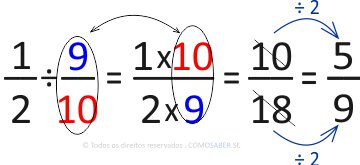
Nesse caso, também simplificamos, pois tanto o 10 quanto 18 são divisíveis por 2.
Exercício 5)

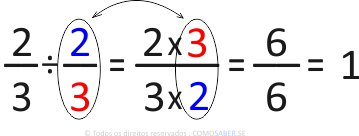
Nesse caso, o resultado foi 1 inteiro, pois a fração resultante foi 6/6, onde 6 ÷ 6 = 1.
- Se for adição de denominadores iguais, some os numeradores e repita o denominador
- Se for adição de denominadores diferentes, tire primeiro o MMC
- Para subtração use exatamente as mesmas 2 regras acima
- Se for multiplicação, é só multiplicar numerador x numerador e denominador x denominador
- Se for divisão, inverta a segunda fração e multiplique
- Em qualquer caso, se tiver fração mista, primeiro transforme ela em fração imprópria
Recomendamos as aulas complementares:
Calcular Porcentagem
Como Calcular Porcentagem: 10 exemplos resolvidosÍndice: Exemplo 1: 200 – 10% Exemplo 2: 25% de 1500 Exemplo 3: 40% de 1200 Exemplo 4: 45 equivale a...
Calculadora de Porcentagem Online – Faça seus Cálculos AQUI!
Calculadora de Porcentagem Online 100% PRÁTICA - Faça seus Cálculos AQUI!Calculadora de porcentagem online para calcular porcentagem de descontos e...
Números Romanos
Números Romanos: Conversor + Tabela Completa até 500.000 Os Números Romanos são compostos por 7 símbolos: I (1), V (5), X (10), L (50), C (100), D...

Tecnólogo em TI SENAI 2010, Técnico em Eletrônica CEFET 2001, professor de inglês, professor de matemática, professor de eletrônica e eletricidade SENAI SC 2006-2011.
 Como Saber Matemática
Como Saber Matemática